Equation of a Line from 2 Points

Starting time, let's see it in activeness. Hither are 2 points (you can drag them) and the equation of the line through them. Explanations follow.

The Points

Nosotros use Cartesian Coordinates to mark a point on a graph by how far along and how far up it is:

graph with point (12,5)
Example: The point (12,5) is 12 units along, and five units up

Steps

There are 3 steps to find the Equation of the Straight Line :

  • 1. Find the slope of the line
  • ii. Put the slope and i point into the "Point-Slope Formula"
  • 3. Simplify

Footstep 1: Find the Slope (or Gradient) from two Points

What is the gradient (or gradient) of this line?

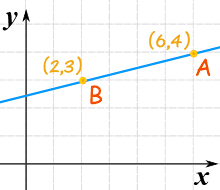
graph 2 points

We know ii points:

  • point "A" is (six,4) (at x is 6, y is iv)
  • bespeak "B" is (ii,iii) (at 10 is 2, y is 3)

The slope is the modify in height divided by the modify in horizontal distance.

Looking at this diagram ...

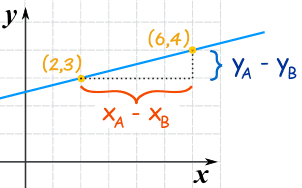
graph 2 points

Gradient m  = alter in y alter in x   = yA − yB tenA − tenB

In other words, nosotros:

  • subtract the Y values,
  • subtract the X values
  • then carve up

Like this:

one thousand  = change in y change in x   = four−3 half dozen−ii   = 1 4 = 0.25

It doesn't thing which betoken comes outset, it notwithstanding works out the same. Try swapping the points:

m  = change in y change in x   = 3−4 2−6   = −1 −4 = 0.25

Aforementioned reply.

Step ii: The "Signal-Gradient Formula"

Now put that slope and 1 betoken into the "Point-Gradient Formula"

graph 2 points

Start with the "signal-slope" formula ( ten1 and y1 are the coordinates of a betoken on the line):

y − y1 = yard(x − tenone)

We can cull whatever point on the line for xone and yi , and so let'south merely utilise point (two,3):

y − 3 = m(x − ii)

We already calculated the gradient "k":

m = alter in y change in x = iv−3 half dozen−2 = i 4

And we have:

y − 3 = one 4 (x − 2)

That is an answer, only we can simplify it further.

Stride 3: Simplify

Starting time with: y − 3 = i 4 (x − 2)

Multiply 1 four and (x−two): y − three = x 4 − 2 4

Add 3 to both sides: y = ten 4 − 2 iv + iii

Simplify: y = x four + v ii

And we become:

y = 10 4 + 5 two

Which is now in the Slope-Intercept (y = mx + b) class.

Check Information technology!

Permit united states of america confirm by testing with the second bespeak (6,four):

y = x/four + 5/two = 6/4 + two.5 = 1.five + 2.5 = four

Yes, when 10=6 then y=four, and then it works!

Another Instance

Case: What is the equation of this line?

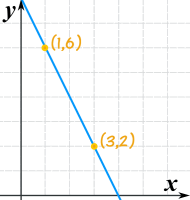
graph 2 points

Kickoff with the "point-slope" formula:

y − y1 = m(x − tenane)

Put in these values:

  • 10ane = 1
  • y1 = 6
  • k = (two−vi)/(three−1) = −4/ii = −2

And we become:

y − 6 = −two(x − 1)

Simplify to Slope-Intercept (y = mx + b) class:

y − 6 = −2x + 2

y = −2x + 8

DONE!

The Big Exception

The previous method works nicely except for ane item case: a vertical line:

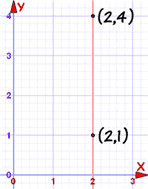
graph vertical line

A vertical line's gradient is undefined (because we cannot separate by 0):

m = yA − yB xA − 10B = 4 − i 2 − 2 = three 0 = undefined

But in that location is still a way of writing the equation: use ten= instead of y=, like this:

x = two