How To Find The Phase Shift Of A Sine Graph

Welcome to Omni's stage shift reckoner, where nosotros'll report trigonometric functions and how to calculate their stage shift. In fact, nosotros'll cover more than that: nosotros'll also explain how to notice the amplitude and how to find the period. Equally a thing of fact, it turns out that a huge class of functions behave virtually the same, and the differences boil downwards to describing the very values mentioned to a higher place; the amplitude, period, and stage shift. Well, upwards to a vertical shift, at least.

The amplitude, catamenia, phase shift, and vertical shift

As we've mentioned above, we'll exist focusing hither on trigonometric functions: more than specifically on the sine and cosine. Still, it's important to retrieve that many of the notions are more than general, specially those of the horizontal translation or the vertical shift.

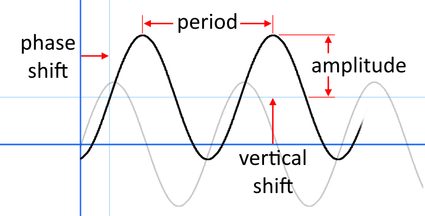
Offset of all, let'due south look at a picture showing where the amplitude, flow, stage shift, and vertical shift announced on the graph (note that the same epitome appears at the top of Omni's stage shift estimator).

We can write such functions with the formula (sometimes called the phase shift equation or the phase shift formula):

• f(x) = A * sin(Bx - C) + D; or
• f(x) = A * cos(Bx - C) + D,

for A, B, C, D arbitrary real numbers, but with A and B not-zero (otherwise, it wouldn't exist a trigonometric role). Patently, those four numbers decide the amplitude, menses, phase shift, and vertical shift. To an extent, the film suggests how they affect the graph. Still, information technology'd be useful to support the visuals with some definitions.

1. The amplitude is how far (either mode) the values run from the graph's centerline. For a simple sine or cosine, its value is 1 since the centerline is at 0, and the part's values range from -1 to ane.
2. The period is the length on the horizontal axis, after which the function begins repeating itself. In other words, the (infinite) graph is simply a bunch of period-length copies glued together at the ends. For a elementary sine or cosine, the period equals 2π since sin(0) = sin(2π) = sin(4π) = ... and the parts in between are exactly the same (and similarly for the cosine).
3. The phase shift (besides called the horizontal shift or horizontal translation) describes how far horizontally the graph has been moved from the regular sine or cosine. Equally such, the value is equal to 0 if nosotros accept the 2 functions unaltered.
4. The vertical shift (also called the vertical translation) describes how far vertically the graph has been moved from the regular sine or cosine. In other words, it's the stage shift's twin that concerns the perpendicular direction. In particular, the value is again equal to 0 if we take the ii functions unaltered.

Alright, nosotros've learned what the stage shift is, besides as the three accompanying values. The sections below describe how to summate each of them based on the annotation from the stage shift formula above. First, we show how to find the amplitude.

How to find the aamplitude

We know that the sine and cosine functions take values ranging from -1 to 1. What is more, that simple fact doesn't change if we substitute sin(x) or cos(x) for sin(Bx - C) or cos(Bx - C) for a not-zippo B and arbitrary C. In fact, it's because the function f(x) = Bx - C is then a bijection (i.e., a one-to-one correspondence) onto the infinite of real numbers.

Now let's see what happens if nosotros add together D, i.eastward., if we have sin(Bx - C) + D or cos(Bx - C) + D instead. Since the offset part gives something between -1 and ane, the whole thing volition be between -ane + D and 1 + D (come across How to observe the vertical shift for comparison). That ways the centerline falls at D, and the amplitude is still 1 considering the values autumn as far as 1 abroad from D.

Therefore, the simply thing that tin can affect the amplitude in the phase shift formulas A * sin(Bx - C) + D and A * cos(Bx - C) + D is the non-nix A. And indeed, since sin(Bx - C) and cos(Bx - C) are all this time between -ane and 1, the multiplier A changes this range to -1 * A = -A and 1 * A = A.

Yup, you guessed it: the amplitude of the phase shift equations A * sin(Bx - C) + D and A * cos(Bx - C) + D is simply equal to A.

How to find the period

Recall that the sine and cosine functions take periods (no, not that kind of period) equal to 2π, i.e., nosotros take sin(10 + 2π) = sin(10) and cos(x + 2π) = cos(x) for whatsoever x. In particular, that gives:

A * sin(x + 2π) + D = A * sin(x) + D and A * cos(ten + 2π) + D = A * cos(x) + D

Then, we see that the A and D in the phase shift formula have no outcome on the period. Indeed, information technology all boils downwardly to what happens inside the trigonometric functions. And however:

sin(x - C + 2π) = sin(ten - C) and cos(x - C + 2π) = cos(x - C),

by the very aforementioned rules every bit in a higher place, so it's not the C either that does the job. So, with three options discarded, it must be the fourth: the B.

We once more turn to the comment we started with to empathize why and how B affects periodicity in the stage shift equations A * sin(Bx - C) + D and A * cos(Bx - C) + D. After all:

sin(Bx) = sin(Bx + 2π) = sin(B * (x + 2π/B)),

And then with every 2π/B added to the argument x, nosotros land back in the same spot, and the office repeats itself (and similarly for the cosine).

All in all, the menstruation of a phase shift equation is equal to 2π/B .

How to find the phase shift

By definition, the phase shift describes the horizontal translation of the function with respect to the regular sin(x) or cos(ten). Every bit such, the bones functions have it equal to 0. In fact, if we compare their graphs:

…we'll notice that we can get one past translating the other (in fact, mutual cofunctions have many similarities). To be precise, we accept:

sin(x + π/2) = cos(ten) and cos(ten - π/2) = sin(ten).

The example above already suggests where in A * sin(Bx - C) + D and A * cos(Bx - C) + D, we should look for the values responsible for phase shifts. However, equally opposed to the aamplitude and period, this time, we'll demand ii of the four letters.

In general, (that is, non only in stage shift equations), we obtain the horizontal translation of an arbitrary function f(x) by calculating f(x - a): the shift of the graph by a to the right. In other words, nosotros substitute every occurrence of 10 with 10 - a in the formula for f(10). For instance, applying the translation to sin(10) gives sin(x - a), merely for, say, cos(3x + 1) nosotros'd go:

cos(3 * (x - a) + 1) = cos(3x - 3a + 1),

i.e., we cannot forget about the multipliers standing in front of x.

In our case, the phase shift formula gives:

A * sin(Bx - C) + D = A * sin(B * (x - C/B)) + D,

which is a phase shift of C/B (to the right) of the function A * sin(Bx). Of form, we can repeat the higher up for the cosine besides.

To sum it all upwardly, in social club to calculate the phase shift of a phase shift equation, you lot need to find C/B .

How to find the vertical shift

This one's piece of cake, particularly now that we've seen what the phase shift, aamplitude, and period are and how to calculate them. Let usa build on what we've learned so far.

We know that in the phase shift formulas A * sin(Bx - C) + D and A * cos(Bx - C) + D, the A determines how far the values fluctuate on either side of the centerline. The B specifies how far we extend the graph's bumps and, every bit a outcome, how fast we get to repeat the values. Also, together with C, the two describe if we've moved the function to the left or right and how much.

Obviously, the horizontal translation doesn't affect the vertical shift: those are two perpendicular directions, after all. On the other paw, the aamplitude just tells usa how far vertically the graph reaches, but it doesn't shift it. All in all, nosotros're left with just i letter: D.

The D in the phase shift equations is precisely the vertical shift. Information technology determines the function's range, i.e., how far from the usual, no-D version we movement the graph.

That concludes the theoretical part for today. It's time to see how to calculate the stage shift on a dainty example. And you know what? Nosotros'll show how to find the flow, the aamplitude, and the vertical shift equally well. After all, why not? More mathematical calculation = more than fun!

Case: using the amplitude flow stage shift calculator

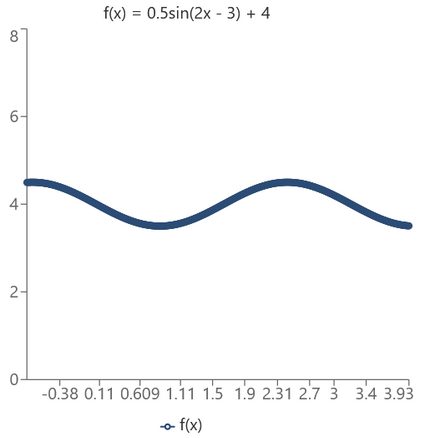
Let'southward see how to find the amplitude, period, stage shift, and vertical shift of the function f(10) = 0.five * sin(2x - 3) + 4. Firstly, we'll permit Omni's phase shift computer do the talking.

At the summit of our tool, we need to cull the role that appears in our formula. In our example, nosotros choose "sine" under "The trigonometric function in f." That'll trigger a symbolic representation of such a phase shift equation: f(x) = A * sin(Bx - C) + D. Looking back at what nosotros have, we input:

A = 0.5, B = 2, C = 3, D = iv.

(Note how fifty-fifty before nosotros input the values, the phase shift calculator displays the graph of the office sin(x). That is considering the tool understands not giving certain values every bit no numbers in the respective places in the formula. As such, it reads no input at all as A = 1, B = 1, C = 0, and D = 0, which gives 1 * sin(1 * x - 0) + 0 = sin(ten).)

The moment we give the last value, the function's graph appears underneath together with the amplitude, menstruation, phase shift, and vertical shift farther down. Also, observe that if needed, you tin go into the advanced mode of the reckoner to discover the office's value at any point x₀.

Now let'south explain how to find the phase shift and all the other values ourselves. For that, information technology'due south enough to recall the four sections higher up to calculate that:

• The amplitude is A = 0.5;
• The period is 2π / B = 2π / ii = π;
• The phase shift is C / B = iii / 2 = 1.5; and
• The vertical shift is D = four.

All in all, the graph looks like this:

A piece of block, wasn't it? Make certain to play around with the phase shift calculator to encounter how different coefficients touch the graph. And once you lot get bored with it, move on to other Omni trig calculators and gear up to accept even more fun!

FAQ

How practise I calculate the phase shift?

To calculate the phase shift of a function of the class A × sin(Bx - C) + D or A × cos(Bx - C) + D, you demand to:

1. Make up one's mind B.
2. Determine C.
3. Divide C / B.
4. Remember that if the effect is:
   • Positive, the graph is shifted to the correct.
   • Negative, the graph is shifted to the left.
5. Enjoy having found the phase shift.

How do I discover the stage shift from a graph?

To find the stage shift from a graph, you lot need to:

1. Determine whether it's a shifted sine or cosine.
2. Look at the graph to the right of the vertical axis.
3. Detect the commencement:
   • Tiptop if the coefficient before the function is positive; or
   • Trough if the coefficient is negative.
4. Summate the distance from the vertical line to that betoken.
5. If the function was a sine, subtract π/ii from that distance.
6. Enjoy having found the phase shift from a graph.

How do I find the aamplitude, period, and phase shift?

Finding the amplitude, flow, and phase shift of a function of the form A × sin(Bx - C) + D or A × cos(Bx - C) + D goes every bit follows:

• The amplitude is equal to A;
• The menstruation is equal to 2π / B; and
• The phase shift is equal to C / B.

How practise I graph trig functions with phase shift?

To graph trig functions with phase shift, you lot demand to:

1. Make up one's mind what the trig function is.
2. Focus on the bespeak (0,0) on the plane.
3. If the phase shift is:
   • Positive, move to the right.
   • Negative, move to the left.
4. Move the distance given by the phase shift.
5. The bespeak yous country in is your starting signal.
6. Draw the non-shifted function's graph as if the signal were (0,0).
7. Enjoy having graphed a trig function with a stage shift.

Are horizontal and phase shift the same?

When it comes to trigonometric functions, yes. Nosotros usually reserve the term "phase shift" for trig functions. In other words, we tin can have a horizontal shift of any graph or part. Withal, when it is, in fact, a trigonometric one, we can equivalently phone call that horizontal shift a phase shift.

Source: https://www.omnicalculator.com/math/phase-shift

Posted by: fileralcull.blogspot.com

Share this post